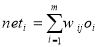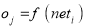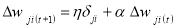Impact of Urban Living on Biodiversity and Ecosystems
| ✅ Paper Type: Free Essay | ✅ Subject: Environmental Studies |
| ✅ Wordcount: 5019 words | ✅ Published: 4th Sep 2017 |
It is estimated that almost more than one half of the world’s population is presently living in urban areas (Sakieh et al. 2016; Weigi et al. 2014). In many parts of the world, increasing urban lands has caused changing land use and land cover (LULC) (Wu 2014). Biodiversity, ecosystem processes and functions and human habitants in an urban environment are influenced by the speed and spatiotemporal pattern of urbanization (Wu et al. 2011; Asgarian et al. 2015; Sangani et al. 2015; Wu 2014; Jaafari et al. 2015). Landscape beauty is being affected by LULC changes and urbanization has led to the destruction of aesthetic values in many parts of the world. Scenic landscapes, as one of the ecosystem services, are elements of the environment with the potential for human enjoyment and in some cases they are considered as valuable parameters for nature conservation and management (Bishop and Hulse 1994). The landscape is continually changing due to human activities but its aesthetics usually suffers from poor quantification and inclusion in management plans. According to Naveh (1995), scenic landscapes are products of interactivity between humans and natural systems where natural landscapes become inhabited, influenced or altered by mutual relationships between ecological and socioeconomic processes. Such interrelated feedbacks can lead to physical modifications of the environment that ultimately can be seen, so landscape aesthetic assessment seem to be essential in land use planning.
If you need assistance with writing your essay, our professional essay writing service is here to help!
Essay Writing ServiceUnderstanding, analysis, monitoring and modeling of urban growth is crucial for the management of current urban systems as well as for the planning of future growth (Zhou et al. 2014). Geospatial predictive models and change detection methods can provide a further level of understanding of the causes and impacts of urban growth mechanisms (Sakieh et al. 2014a). In the process of decision making, land managers need to examine the consequences of the urban development process. Regarding the progress in computing power, easy access to spatial data sets and development of functional computer-based models, now there is a possibility in which land use managers and decision makers can evaluate the outcome of their decisions under different alternatives and at the minimum possible cost (Sakieh et al. 2014b). Inclusion of new methodologies such as spatial multi-criteria evaluation (SMCE) can further improve representation and modelling of urban growth patterns, which finally provide spatial decision support systems (SDSS) for better planning and management of urban areas (Dai et al. 2001; Jie et al. 2010; Youssef et al. 2011; Xu et al. 2011; Pourebrahim et al. 2011; Yuechen et al. 2011; Bagheri et al. 2013; Bathrellos et al. 2012; Sheng et al. 2012; Jeong et al. 2013, Sakieh et al. 2014b).
Since 2000, there have been noticeable efforts for developing microsimulation LULC change methods such as cellular automata (CA) and agent-based models (Goodarzi et al.2016). CA-based models have a natural compatibility to raster geographic information system (GIS) and remote sensing (RS) data and are appropriate for detail resolution modeling and simulating dynamic spatial processes (Sullivan and Torrens 2000). In recent years, there have been developed some CA-based models such as SLEUTH (Slope, Landuse, Exclusion, Urban, Transportation, and Hillshade) (Clarke et al. 1997), CLUE-S (the Conversion of Land Use and its Effects at Small regional extent) (Verburg et al. 2002), iCity (Stevens et al. 2007) and DINAMICA (Soares-Filho et al. 2002). Compared with the above mentioned spatial models, the SLEUTH model requires fewer input layers and also offers various alternatives for future urban growth prediction (Norman et al. 2012). These characteristics of SLEUTH model have made it as one of the most-implemented and popular methods for land use simulation at different scales (e.g. regional, national, and even binational) (Maithani 2010; Norman et al. 2012; Chaudhuri and Clarke 2013). However, there are a number of limitations with SLEUTH. The first of these is that it is computationally expensive. It requires a high number of model runs using a multi-stage calibration process to narrow down the coefficient value for each input parameter (Goldstein 2003). The second drawback is related to non-linearity of the model for the combination of the coefficients. The Brute Force method[1] which is used in this paper for calibrating the SLEUTH can fall in local maxima and may miss the better coefficient set (Goldstein 2003, Jafarnejad et al. 2015).
Urban expansion is a complicated event which mainly occurs because of increasing population and the need for more construction. Consequently, vast lands of valuable ecosystems such as agricultural lands, forests and pastures are consumed and converted to urban areas (Sakieh et al. 2014b). Therefore it is essential to understand and recognize this process in order to implement effective management and avoid reducing the aesthetic value of landscapes. To achieve this goal, areas with high aesthetic value should be recognized at the first step. In this regard, there are various approaches to determine the aesthetic impacts on different areas of the city including expert-based methods such as Multi-Criteria Evaluation (MCE), statistical approaches such Logistic Regression (LR) and Artificial Intelligence-based methods such as Multi-Layer Perceptron (MLP) Neural Networks (Riveira and Maseda 2006). These methods are repeatedly being implemented for suitability mapping of utilities such as urbanization (Pijanowski et al. 2002; Hu and Lo 2007; Pao 2008; Mahiny and Clarke 2012; Sakieh et al. 2015), environmental conservation (Singh and Kushwaha 2011; Mehri et al. 2014; Sakieh et al. 2015) and agricultural activities (Mozumder and Tripathi 2014; Bodaghabadi et al. 2015) but are less implemented for mapping aesthetic values. The MLP neural network approach has a remarkable ability to derive meaning from complicated or imprecise data and detect trends that are too complex for either humans or other computer techniques. MLP is a more accurate modelling method compared to the others (Saeidi and Salmanmahiny 2014) and has been used in this research. Accordingly, creating a suitable model to predict the landscape scenic value could provide a basis for explicit, quick and accurate integration of aesthetic evaluation into land-use planning efforts. Therefore, the main objective of this study is to evaluate the landscape aesthetic suitability and predict the spatial patterns of urbanized lands in an effort to preserve landscapes of high aesthetic value.
The following section describes how a directed modeling framework can be employed to introduce urban growth scenarios with regarding landscape aesthetic suitability, and finally to develop a city without considerable impact on its aesthetic suitability.
Materials and methods
Study area
Gorgan is one of the cities in the northeast of Iran and the capital of Golestan province, located in 36°, 49´ N and 54°, 24´ E (Fig. 1). Gorgan has a mild and humid climate though summers are very hot and humid. The regional topography is very diverse and includes mountains, forests and grasslands, steppes and plains, desert and barren, rivers, wetlands and agricultural lands. Lush Hyrcanian temperate forests are located in the south, while flat areas with farmlands and rangelands make the main structure of the landscape in the north part of the case study. the region is also a destination for about two millions of tourists each year because of its aesthetic values and touristic environment, (Mehrnews 2015).Regarding the nomination of the area as a new province of Iran, rapid population growth has occurred that caused the increasing of built-up surfaces and consequently has made a series of conflicts between land developers and conservation agencies. These disagreements emphasise the importance of LULC planning in this area (Sakieh et al. 2016 b).
Figure (1)
Scenario based urban growth modelling
In this research the SLEUTH cellular automata urban growth model was used to predict dynamics of Gorgan City developing under three different scenarios including historical, managed and aesthetically sound urban growth up to year 2030. The Historical Urban Growth (HUG) scenario assumes that the present pattern of urban growth will be maintained in the future. At the Managed Urban Growth (MUG) scenario, we tried to dictate an infill form of urban development with the aim of protecting the immediate environment of the city against urbanization. In the Aesthetically sound Urban Growth (AUG) scenario, an aesthetic suitability layer was used as the extra excluded layer in SLEUTH model to protect patches of high scenic value. Fig. 2 depicts a research flowchart of the study. The procedure for determining the aesthetic suitability map which was used as the excluded layer is explained in the following section.
Figure (2)
Aesthetic suitability mapping using MLP
MLP is a feed forward artificial neural network model that maps different sets of input data toward a set of applicable and meaningful outputs (Rumelhart 1986). In a feed forward neural network, the information moves only in forward direction, from the input nodes, over the hidden nodes and to the output nodes. A node is considered to be a connection point that can receive, create, store or send data along distributed network routes (Ciresan et al. 2012). Exclusive of the input nodes, each node is a neuron or processing element with a nonlinear transfer function (Fig. 3). There are no cycles or loops in the network. MLP utilizes a supervised learning technique called back propagation for training the network (Rosenblatt et al. 1961; Rumelhart 1986). Learning process conducts in the perceptron by changing the connection weights after the processing of each part of data.
Figure (3)
Back propagation includes two main stages, forward and backward propagation, to achieve its modification of the neural status. During model training, each sample (e.g. a feature vector related to a single pixel) is entered into the input layer and the receiving node sums the weighted signals from all nodes to which it is connected in the former layer. In this regard, the input to a single node is weighted based on the following equation:
|
|
Eq. (1) |
given:
wij indicates the weight between node i and node j and o is the output from node i. The result from a given node is j is then computed from:
|
|
Eq. (2) |
Function f is often a non-linear sigmoidal transformation that is used to weight the sum of inputs before it sends a signal to the next node. When the forward pass is finished, the performance of the resultant nodes are compared with their corresponding expected values. When a pattern is given to the network, each output node will differ from the preferred results, the difference is linked to the error in the network as well. This error is then propagated backward with weights for corresponding connections modified using a relation known as the delta rule:
|
|
Eq. (3) |
Given: η is the learning rate of the model; δ is the computed error; and α is the momentum factor. This factor intends to avoid oscillation problems during the search for the minimum value on the error surface and is used to speed up the convergence procedure (Richards et al. 1999).
The forward and backward passes continue until the network is properly trained for the characteristics of the targeted utility which in this research is the scenic beauty. Model training is aimed to retrieve the correct weights both for the connections between the input and hidden layers, and between the hidden and the output layer for the categorization of the unknown pixels. The input pattern is categorized to a class that possesses the node with the greatest activation level.
The two training elements, automatic training and dynamic, can be employed to automatically execute the MLP. If one or both are used, the training procedure automatically restarts when the algorithm is highly oscillated or become trapped in a local minimum error surface. For each automatic restart of the model training procedure, one of the following items occurs to either learning rate or the sample used in the training procedure, or both.
- If only automatic training is selected and the first occurrence that the training procedure restarts, the starting weights are randomized. Through the next restarts, the weights are randomized and the learning rate is halved.
- If both automatic training and dynamic learning rate are chosen and the training restarts automatically, new samples are selected, the weights are randomized, and the learning rate splits in half.
- If only dynamic rate is chosen, and the learning rate is progressively lowered based on the number of iterations assigned and the start and end learning rates. For instance, if 10,000 iterations are specified and the model is configured with start rate of 0.1 and end rate of 0.001, it will divide 0.009 by 10,000 and lower the learning rate by the result at each iteration (Civco 1993).
The acceptable error rate is related to the learning of the network and it is assessed based on the Root Mean Square (RMS error). Lower values of RMS error and higher values of total r2 shows the better fit of model.
The MLP algorithm can produce both a hard and soft classifier. The hard classification output generates a discrete layer in which each cell belongs to a definitive category. Activation level maps, however, unlike the output of the hard classifier, are a series of images depicting a degree of membership for each pixel to each possible category. The output is set of images (one per class). Unlike the probability map, the sum of values for any location will not necessarily sum to 1. This is because the results from the neural network are acquired through standardizing the signal values in the range of 0-1 with the activation equation. Larger values imply a higher membership degree of the membership belonging to that corresponding category. The computation of the hard classification result is on the basis of the activation level maps.
Data used for aesthetic suitability modelling through MLP method
In the MLP analysis of the targeted area, multiple of factors were considered as input layers. Due to the characteristics of Gorgan City, a set of urban and natural criteria was used to model its landscape aesthetic values. These criteria were outlined during previous studies performed in our research area included gardens and agricultural lands (Othman et al, 2015; Mobargheie and Torbati 2014), tree type diversity, vegetation density (Aminzadeh et al, 2014; Weiqi et al, 2014; Chen et al, 2014; Kremer et al, 2016; Martina et al, 2016), topographic diversity (Arrowsmith 2001), buildings height and density (Weiqi et al. 2014; Chen et al. 2014), forest and urban parks (Ayad 2005; Weiqi et al. 2014), ancient sites and squares, refuges and boulevards (Bahrainy 1999; Aminzadeh et al. 2014).
The GIS layers of gardens and agricultural lands, parks, squares, boulevards and refuges were obtained from the land use map maintained by the Gorgan municipality. The values of cells within these layers, together with ancient sites, were standardized using a user-defined function and based on the experts’ opinions. Whereas the relationship between the map value and fuzzy membership did not follow a certain function (e.g. linear, J-shaped or Sigmoidal), the user-defined function was the most applicable function and the user could reclass the map in the standard range.
The ancient sites layer was obtained from Department of Cultural Heritage, Crafts and Tourism of Golestan province.
The tree type for the study area consisted of six categories of tree communities (scale 1:25,000). Pattern analysis (with window size of 3 Ã- 3 pixels = 8100 m2) was applied as a filter to count the number of various classes inner a square vicinity of the central cell. Those pixels with three or more different categories in their vicinity were chosen to represent the diversity of a given location for its tree types.
By using a Landsat TM image for the study area for 2012, vegetation density was calculated using the Normalized Difference Vegetation Index (NDVI) formula:
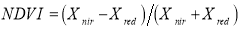 Eq (4)
Eq (4)
NDVI is a widely used graphical indicator that can be used for detecting vegetative land cover. This index can be calculated based on red and near-infra-red (Xred, Xnir) spectral bands of Landsat image as equation 4 (McFeeters 1996). The layer was standardized using a symmetrical linear function having inflection values as: a=2879, b=5795, c=7595 and d=9545 (Fig. 4).
Figure.(4)
As the graph shows, by increasing the vegetation density (that is increasing NDVI values) to the point b, scenic value of landscape increases, then in a specific area remains constant (point c) then over increasing of the vegetation density due to restrictions in visibility detracts from scenic value of landscape.
The building height and density layer was produced using the current status map of building density provided by the Gorgan municipality. Using a monotonically decreasing linear function in order to determine classification, this layer was standardized. The landscape aesthetic value was therefore decreased by increasing the building height and density, due to the viewshed being blocked.
In the spatial input factors, a topographic diversity layer was also included. To determine this layer, a Digital Elevation Model (DEM) of the research area was acquired from National Cartographic Centre of Iran. A surface shape categorisation was performed on a DEM layer, which consisted of multiple topographic features: peak, flat, ravine, pit, ridge, saddle, slope hillside, saddle hillside, convex hillside, concave hillside and inflection hillside. The categorized layer was then analysed using a mode filter (window size of 3 Ã- 3 pixels) to specify a new score to the central cell based on most frequent values within the window. Then, a filter size of 7 Ã- 7 pixels was used to count the number of various categories within the neighbourhood of a central pixel to achieve the final map. This layer demonstrates the most diversified locations in terms of topographic features. The layer was standardized using a monotonically increasing linear function, whereby categories with higher diversity got the higher score in the standardised value. Fig. 5 portrays factor layers used for aesthetic suitability mapping in this study.
Figure (5)
After preparing required inputs, the MLP model was configured according to the following data:
Input variables: number of input variables = 8 (standardized factor maps)
Input specifications: training points file = a raster map of 164 points, which retains the location of 164 attractive (99) and non-attractive (65) spots | maximum training pixels used = 200 | maximum testing pixels used = 200
Network topology: input layer nodes: 8 (equals to the number of input data) | output layer nodes = 1 (continuous surface of aesthetic suitability) | hidden layers =1 | hidden layer nodes = 16
Training parameters: the dynamic learning rate was employed | start learning rate = 0.01 | end learning rate = 0.001 | Momentum factor = 0. 5 | sigmoid constant a = 1.0
Stopping criteria: root mean square (RMS) error = 0.01 | iterations = 10,000
Output function = sigmoidal
Once the model was trained, its performance was evaluated by plotting training RMS versus testing RMS during 10,000 model iterations. Lower values for testing error during iterations indicates proper training of the model, and therefore, it can be used to produce aesthetic suitability surface.
Data processing for SLEUTH modeling
For the SLEUTH modeling undertaken in this study, four urban extent years depicting the distribution of manmade features over time, two layers of the transportation network for two different time periods, one excluded “aesthetics” layer from urbanization, slope and hillshade layers were used. These input data layers were prepared by the integrated application of geographic information systems and remote sensing. As a model requirement, all binary urban/non-urban layers were stretched linearly and converted into a GIF format. The urban and transportation layers were created based on Landsat MSS and TM images for the years 1987, 1992, 2000 and 2010. These were then used to predict the expansion of Gorgan in 2030. Using a 30-m digital elevation model (DEM), slope percent and hillshade layers were derived. For the first and second modeled scenarios, hydrographical networks (rivers, dams and wetlands), dense forests and roads were used as excluded layers from urban growth. For the third scenario, the aesthetic layer was added as an exclusory layer. These are shown in Fig. 6.
Figure (6)
Model calibration
SLEUTH is a CA-based model in which five coefficients (diffusion, breed, spread, slope and road gravity) control four types of growth rules including new spreading center growth, spontaneous growth, edge growth and road gravity growth (Jantz et al. 2014). In addition, the straightforward calibration method applied by SLEUTH makes it adaptable to any particular geographic area over time (Clarke et al. 1996). In order to show the relative importance, each coefficient has a dimensionless value ranging between 0 (least important) to 100 (most important). During the calibration process, the form of urban expansion was detected via the four growth rules. The prediction of the model was based on the best range of refined coefficients derived from the calibration step. Table (1) shows the relationships between growth types and growth coefficients.
Table (1)
The main assumption of the SLEUTH model is based on the inherent pattern of urban dynamics whereby the city will witness the same growth in the future based on its historical trend in the past (Clarke et al. 1997). During the calibration process, the model seeks to derive the best range for each coefficient to enable better simulation based on local historical data (Silva and Clarke 2002). SLEUTH model benefits from a stochastic computation algorithm known as the Monte Carlo method. The model utilizes Monte Carlo iterations stochastically to generate multiple simulations of urban growth so parameters are standardized in a range between 0 and 100. These inputs reflect the relative contribution of each parameter to the dynamics of urban growth in the study area (Sakieh et al. 2014b). Finally, by using the best set of derived coefficients from three steps (coarse, fine and final) of calibration, the model was executed for the simulation of the historical data set. The number of Monte Carlo iterations support the robustness of final coefficients to run the prediction part of the model (Candau 2002; Jantz et al. 2004; Sakieh et al. 2014b). For the coarse calibration step, the default parameter values from the sample calibration scenario were employed. Five Monte Carlo iterations were specified for the coarse calibration phase, and growth parameters were set at their widest range of 0 – 25 – 100 as START, STEP and STOP values, respectively. A goodness of fit metric, known as the Optimal SLEUTH Metric (OSM) will provide the most robust results for SLEUTH calibration. The OSM is the product of the compare, population, edges, clusters, slope, X-mean, and Y-mean metrics (Dietzel and Clarke 2007). These seven metrics range between 0 and 1 and are multiplied together to calculate the OSM. The iterations are then sorted based on this metric and the best ranges of performing coefficients are chosen for the subsequent calibration stage. Applying the OSM metrics of the best performing iterations, the five multipliers were refined and reduced for use in the fine calibration step. The fine calibration step was executed through full resolution input layers in eight Monte Carlo iterations. Based on OSM values, the ranges for the five growth parameters in SLEUTH were further narrowed for the final phase of the calibration mode, which used 10 Monte Carlo iterations. Finally, the ranges for averaging values of the five coefficients of urban development in SLEUTH were set and the averaging was run for 100 Monte Carlo iterations.
Model prediction
After the calibration and performance validation of the model, the prediction step was executed using the entire data coverage and 100 Monte Carlo iterations. Prediction of the model was based on the initial seed year of the current urban pattern, using those refined values of coefficients. The output of the SLEUTH model is a continues surface in which each cell has a probability value to become an urbanized space in the future. This map is produced for every year including the first year (1987) to the last year (2030).
Our academic experts are ready and waiting to assist with any writing project you may have. From simple essay plans, through to full dissertations, you can guarantee we have a service perfectly matched to your needs.
View our servicesThere are three different methods used to simulate the expansion of urban area under different scenarios in the SLEUTH model. In the first method, best-ï¬t multipliers derived from the calibration phases can be altered (Leao et al. 2004; Rafiee et al. 2009) and consequently the growth rules will change. In the second method, the excluded layer is weighted through a continuous range of resistance values against urbanization to show that even cells within the excluded layer have the potential to be urbanized under different probabilities (Oguz et al. 2007; Jantz et al. 2010; Mahiny and Clarke 2012, 2013). In the third method, the constraints of self-organization can be modiï¬ed (Yang and Lo 2003; Xi et al. 2009). In this study, the first and the second methods were applied for two scenarios. The coefficients were altered in the MUG and AUG scenarios and an aesthetic suitability map of the study area was also used as an extra excluded layer in the AUG scenario. In this case, the historical trend of the urban growth and two different scenarios were forecasted (Table 2). The adopted scenarios in this study used additional information regarding the study area and its development in the past. In addition, it was acknowledged that land use plans are mostly controlled by master plans for cities derived from regional land use planning (Makhdoum 2001; Dezhkam et al. 2014). The adopted scenarios were set up according to assumptions of uncontrolled and controlled growth, which allows decision makers to construct a quantitative comparative basis for evaluation of different growth alternatives. After calibration of the model, scenarios were introduced to model urban growth to the year 2030 by using two methods of parameter modification and the inclusion of the hydrology, dense forest and transportation exclusion layers in the first two scenarios as well as aesthetic exclusion layers in the third scenario.
Table (2)
The first scenario assumed that the present pattern of urban growth will be maintained in the future, and therefore, the originally derived parameters were used. The first exclusion layer including hydrographical networks, dense forests and roads were used for this. The prediction was conducted by means of the same resolution data and 100 Monte Carlos iterations.
The second scenario used the same exclusion layer as the HUG scenario, but spread and breed coefficients were reduced (from 30 and 59 to 20 and 40 respectively) to dictate an infill urban development with the aim of protecting the immediate environment of the city against urbanization. The slope resistance coefficient was decreased to one-half of its original value, to reflect the current status of urbanization in Gorgan City which shows increasing development on steeper slopes.
The third scenario (AUG) used the same coefficient values as those used for the MUG simulation, but the aesthetic suitability layer was used as an extra excluded layer to protect areas of high aesthetic value.
The output from the SLEUTH model is a probability map, which shows the probability of each single pixel becoming urbanized. In order to produce a clear map that indicates future urbanized areas, a 90 % value was taken as a threshold to depict those cells which were considered most probable ones to become urbanized by 2030.
[1] Brute Force refers to any of several problem-solving methods involving the evaluation of multiple possible answers (urban growth patterns) for model fitness.
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please:
 GBR
GBR